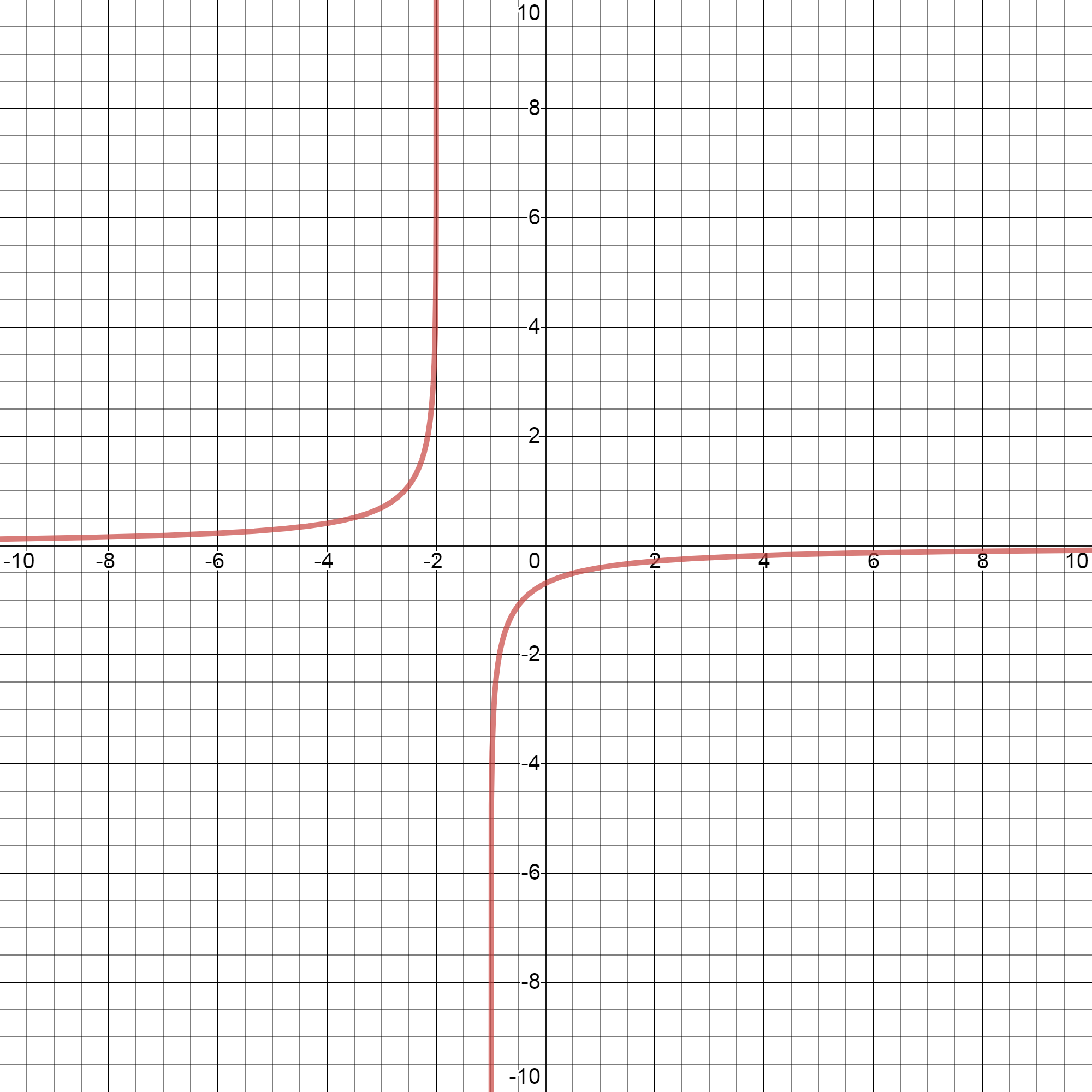
Функсияи \(y = \ln{\frac{x+1}{x+2}}\) таҳқиқ карда шавад.
Ҳал.
1. Соҳаи муайянӣ
Он қиматҳое, ки \(x\) қабул карда метавонад. Азбаски функсия - функсияи логарифмӣ, пас бояд:
\(\frac{x+1}{x+2} \gt 0 \Rightarrow (x+1) \cdot (x+2) \gt 0 \Rightarrow D(y) = (-\infty; -2) \cup (-1; +\infty)\)
2. Соҳаи қиматҳо
\(E(y) = (-\infty; +\infty)\). Ёфтани соҳаи қиматҳо ба пункти 9 вобастагӣ дорад.
3. Оё функсия маҳдуд аст, ё не?
Функсияи зерин маҳдуд нест. Аз пункти 2 бармеояд.
4. Қиматҳои калонтарин ва хурдатирини функсия
Барои ёфтани қиматҳои хурдтарин ва калонтарин, мо бояд ҳосилаи функсияро ёбем:
$$y'=(\ln{\frac{x+1}{x+2}})'=\frac{x+2}{x+1}\cdot(\frac{x+1}{x+2})'=\frac{x+2}{x+1}\cdot \frac{x+2-(x+1)}{(x+2)^2}=$$
$$=\frac{1}{x+1}\cdot\frac{x+2-x-1}{x+2}=\frac{1}{(x+1)\cdot(x+2)}$$
Яъне, \(y'=\frac{1}{(x+1)\cdot(x+2)}\). Барои ёфтани калонтарин ва хурдтарин қиматҳои функсия, мо бояд экстремумҳои ин функсияро ёбем. Барои ёфтани экстремумҳо, мо нуқтаҳои буриши ҳосилаи функсия ва хатти \(Ox\)-ро меёбем.
$$y'=0 \Rightarrow \frac{1}{(x+1)\cdot(x+2)}=0 \Rightarrow \emptyset$$.
Яъне, функсия экстремум надорад.
5. Даври функсия
Функсияи \(y = \ln{\frac{x+1}{x+2}}\) даврӣ нест.
6. Функсияи зерин ҷуфт ё тоқ?
Барои муайян кардани ҷуфт ё тоқ будани функсия, мо бояд \(f(-x)\)-ро ёбем.
$$f(-x)=\ln{\frac{-x+1}{-x+2}}=\ln{\frac{x-1}{x-2}}$$
Азбаски \(f(-x) \neq f(x)\) ва \(f(-x) \neq -f(x)\), пас функсия на ҷуфту на тоқ.
7. Фосилаҳои афзуншавӣ ва камшавии функсия
Барои ёфтани фосилаҳои афзуншавӣ ва камшавӣ, мо бояд ҳосилаи функсия(ки дар пункти 4 ёфта будем)-ро бо сифр муқоиса кунем. Ҳангоми ҳосилаи функсия аз сифр калон будан, функсия афзуншаванда ва ҳангоми аз сифр хурд будан, функсия камшаванда ҳисобида мешавад. Азбаски \(y'=\frac{1}{(x+1)\cdot(x+2)}\) ва \(\frac{1}{(x+1)\cdot(x+2)}\gt0\) дар тамоми соҳаи муайянии функсия, пас ҳангоми \(x \in D(y)\) будан, функсия афзуншаванда мебошад.
8. Буриш бо \(Ox\) ва \(Oy\)
Буриш бо \(Oy\)-ро меёбем. Барои ин мо бояд \(f(0)\)-ро ҳисоб кунем. $$f(0)=\ln{\frac{0+1}{0+2}}=\ln{\frac{1}{2}}=-\ln{2}$$
Яъне, дар нуқтаи \((0; -\ln{2})\) функсия хатти \(Oy\)-ро мебурад.
Барои ёфтани буриш бо \(Ox\), мо бояд муодилаи $$y=\ln{\frac{x+1}{x+2}}=0-ро$$ ҳал кунем.
$$\ln{\frac{x+1}{x+2}}=0 \Rightarrow \frac{x+1}{x+2}=1 \Rightarrow x+1=x+2 \Rightarrow \emptyset$$
Яъне, функсия буруш бо хатти \(Ox\) надорад.
9. Графики функсия